Perceptrons

↑ Top

Introduction

Note: This is a rewrite of an earlier version. I didn’t like the tone of this series, as it felt “off” when compared to the rest of my blog. So I’ve rewritten it.

Hello there. Those of you who have worked directly with me, or just happen to know me through other means, know that I’ve been doing a part-time undergraduate degree alongside my full-time work since 2019. I’ve thoroughly enjoyed it, in particular the third-year module on artificial intelligence (AI) and machine learning (ML). So much in fact that my final year project saw me create my own chatbot.

This was well-timed, as alongside the module I did some quite interesting AI/ML work professionally as well.

As I wrap up my degree, and see AI/ML growing in popularity, I figured I’d explore the foundational concepts that make AI/ML what it is and how this impacts productionisation of such systems in industry.

So we’ll begin with the Perceptron. A simple model made in 1958 by Frank Rosenblatt that, quite frankly, laid the foundation for all the AI gubbins you see knocking about today.

---

The Goal

By the end of this article, you’ll understand:

• What it means for data to be linearly separable and why that matters for perceptrons.
• How a perceptron processes inputs using weights, bias, and summation.
• How the step activation function enables binary classification.
• Why single‑layer perceptrons fail on non‑linear problems (like XOR) and why that matters for modern neural networks.

---

What Does It Mean for Data to Be Linearly Separable?

Before we open up the perceptron, we need to understand the kinds of problems it was designed to solve. But to understand that, we need to understand linear separability.

Defining Linear Separability

Data is linearly separable if you can draw a straight line (in 2D), a plane (in 3D), or a hyperplane (in higher dimensions) that perfectly divides two classes of points: everything on one side belongs to Class A, everything on the other belongs to Class B.

Think about when you were picked last for the football team in PE class. One side of the gym had team 1, the other side had team 2. They were linearly separable.

Visualising Linear Separation

Imagine plotting two types of points:

• Red circles = Class A
• Blue circles = Class B

If you can separate them with a single straight line, the dataset is linearly separable.

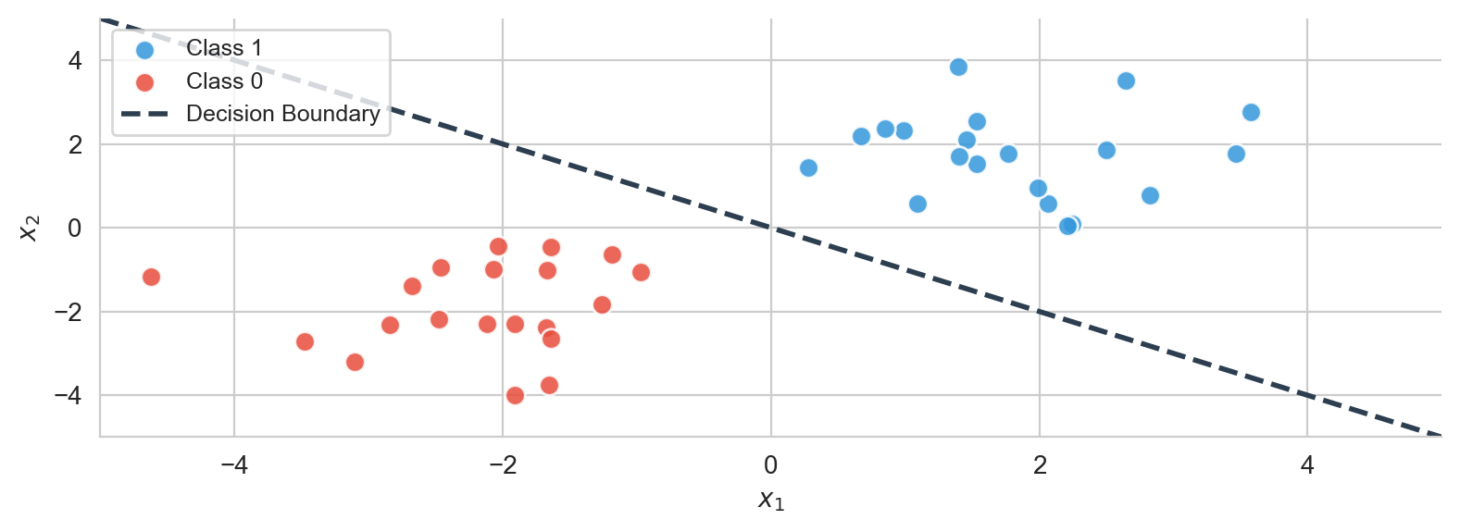
In 3D, this becomes a plane. In higher dimensions (where most machine learning happens), it becomes a hyperplane.

Why Linear Separability Matters

A single‑layer perceptron can only handle linearly separable data. If the classes are arranged so that no single line (or plane) can divide them, the perceptron fails.

One of the simplest examples of non-linearly separable data is XOR, which I’ll natter on about next.

---

Non-linearly separable data (XOR)

Not all data is linearly separable.

Consider an exclusive or (XOR):

• If one input is “on” (1) and the other is “off” (0), the output is 1.
• If both are on or both are off, the output is 0.

This creates a checkerboard pattern that no single straight line can separate.

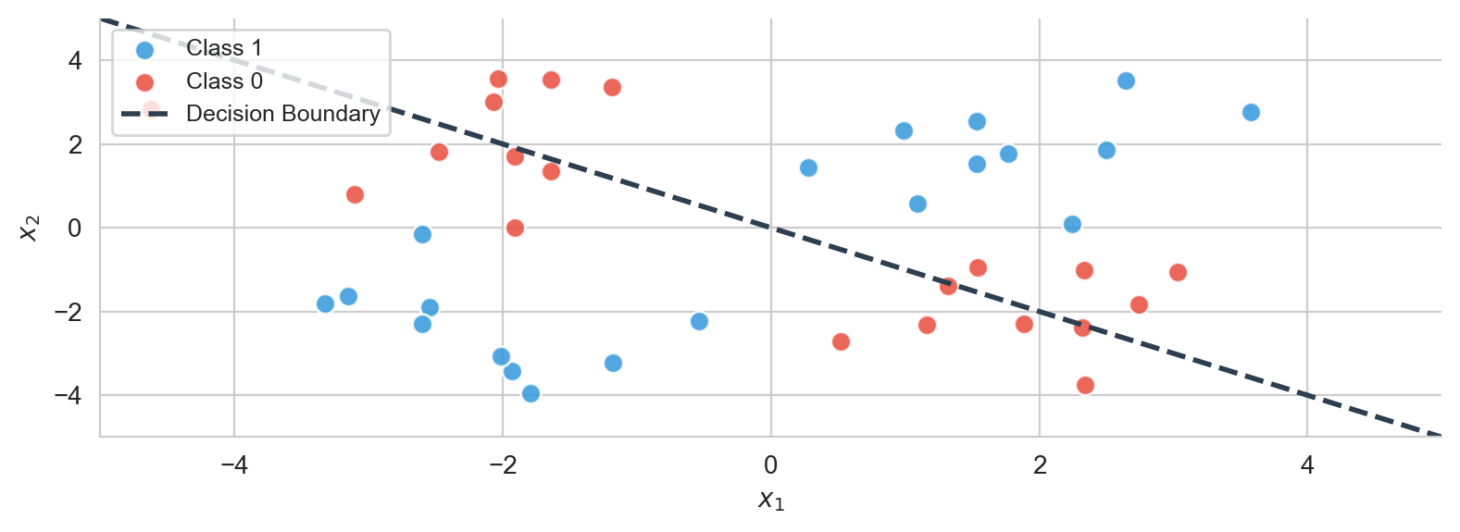
In 3D, the same idea holds: the classes are interwoven so no plane can divide them.

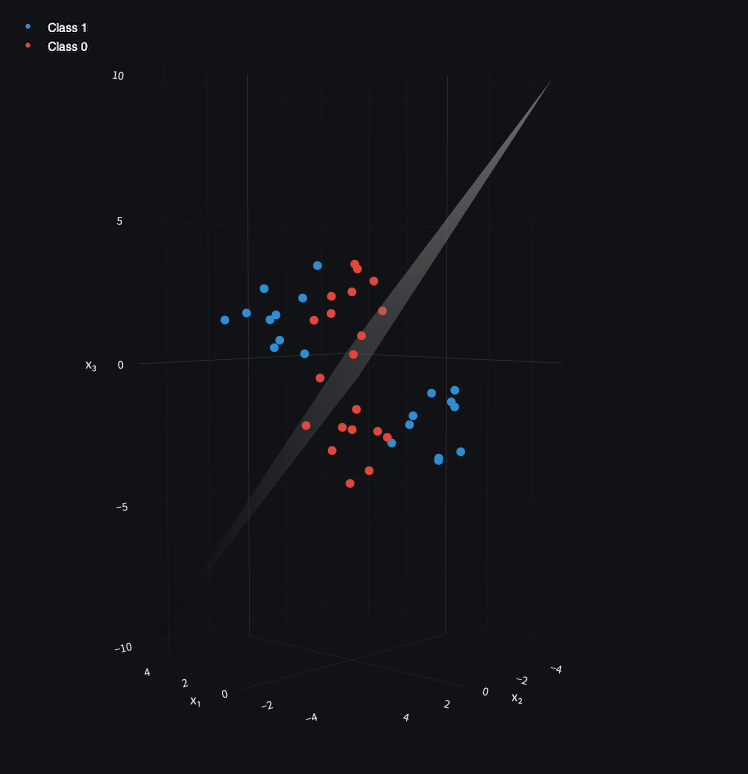
XOR data is extremely valuable, and useful. Any electronics student will tell you XOR gates are fundamental components for binary addition. More “real-life” examples may be found in mutually exclusive actions. For example, you’ve just had a wonderful dinner and you’re torn between the cheesecake or sticky toffee pudding for dessert:

• You may choose the cheesecake (1) and not the sticky toffee pudding (0) (wrong choice in my opinion but still).
• You may choose the sticky toffee pudding (1) and not the cheesecake (0).
• Choosing the sticky toffee pudding (1) and the cheesecake (1) is a mistake you’ll probably regret later.

The Perceptron only works on linearly separable data. It can tell you if you’re looking at a cheesecake or sticky toffee pudding, but it can’t tell you if you should eat one, the other, or both.

---

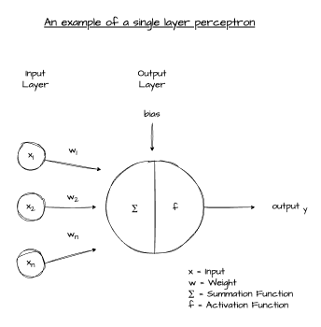
Perceptron Structure

Now that we know what problems perceptrons solve (namely, linearly separable data), let’s look inside at how it functions.

• A Perceptron is a linear classifier.
• It maps input features to a binary output, by computing a weighting sum of features and adding some form of bias.
• The result of this summation is then passed through a threshold-based activation function.

In short. It takes inputs, sums them up, and outputs a “yes” or “no”.

Inputs, Weights and Bias

• Inputs are the numeric values the perceptron needs to consider when performing binary classification.
• Weights are the perceptron’s own views on which inputs matter most.
• Bias is another learned value, which shifts the overall result up or down.

All ML operates solely on numeric data. It’s outside the scope of this post to go over how we represent real-world data numerically (though I might write that up at some point, as it’s an interesting topic in and of itself) so let’s just use some arbitrary data as an example.

We’re still deciding on whether to choose the cheesecake or sticky toffee pudding from earlier, but to make it linearly separate a 1 represents “eat cheesecake” and a 0 represents “eat sticky toffee pudding”.

• In more complex models (which I’ll cover later in the series), the inputs may be matrices, representing images of the cheesecake and sticky toffee pudding. However, a Perceptron is simpler and operates solely on a flat vector of values. For our example, we’ll assume each value is one RGB channel of one pixel:

cheesecake = [24, 245, 235, 133, 147, 89, 123, 168, 1,
              178, 34, 103, 64, 165, 157, 92, 52, 30,
              57, 150, 228, 95, 220, 229, 36, 19, 16]

sticky_toffee_pudding = [131, 190, 14, 119, 48, 105, 43, 64, 140,
                         251, 130, 77, 17, 179, 239, 15, 113, 48,
                         149, 26, 133, 244, 151, 108, 30, 24, 69]

• The weights representing how “important” each input value is for the overall decision. Each “input” corresponds to exactly one “weight”:

weights = [6, 0, 0, 8, 9, 3, 4, 5, 4,
           9, 1, 3, 9, 10, 5, 6, 3, 7,
           0, 7, 6, 9, 5, 7, 8, 8, 7]

• The bias for our image is simply an additive placed after the summation, and before the activation, to influence the result. If 1 means “eat cheesecake” and 0 means “eat sticky toffee pudding”:

bias = -10

As I like sticky toffee pudding a lot, my own bias is -10. i.e. regardless of other factors, this means the perceptron learns towards predicting sticky toffee pudding (0) unless the weighted sum of inputs strongly favours cheesecake (1)

---

Dot Product (aka matrix multiplication)

However, all of these numbers and numeric values are a little meaningless unless we do something with them.

The core “doing” of a perceptron comes in the form of a dot product:

• Inputs and weights are just vectors, i.e. ordered lists of numbers.
• A dot product multiplies two vectors, element-by-element, and adds the results.

For example:

$$\begin{aligned} \mathbf{x} &= \begin{bmatrix} 0.5 & 0.8 & 0.2 \end{bmatrix} \\ \mathbf{w} &= \begin{bmatrix} 1.0 \\ 0.5 \\ 0.2 \end{bmatrix} \end{aligned}$$

Dot product:

$$\mathbf{w}^\top \mathbf{x} = (0.5 \cdot 1.0) + (0.8 \cdot 0.5) + (0.2 \cdot 0.2) = 0.94$$

A dot-product operation, in the context of a perceptron, projects the inputs and weights into a singular meaningful score that may then be fed to the activation function to achieve a result.

---

Summation

Once the dot product of the inputs and weights are computed, the perceptron simply adds whatever bias it has learned (or been programmed with) and we get the base score for decision making.

The perceptron’s weighted sum:

$$z = \mathbf{w}^\top \mathbf{x} + b$$

Where:

• $\mathbf{w}$ = weights
• $\mathbf{x}$ = inputs
• $b$ = bias

---

The Step Activation Function

Turning the $z$ value into some form of output is the job of the activation function.

Activation functions take $z$ and turn them into some form of output. Perceptrons output binary decisions, and thus they utilise the step activation function:

$$f(z) = \begin{cases} 1 & \text{if } z \geq \theta \\ 0 & \text{if } z < \theta \end{cases}$$

If $z$ crosses the threshold $\theta$, the perceptron outputs 1. Otherwise, it outputs 0. Hence, the term “step”; the output steps up from 0 to 1 once you cross the threshold.

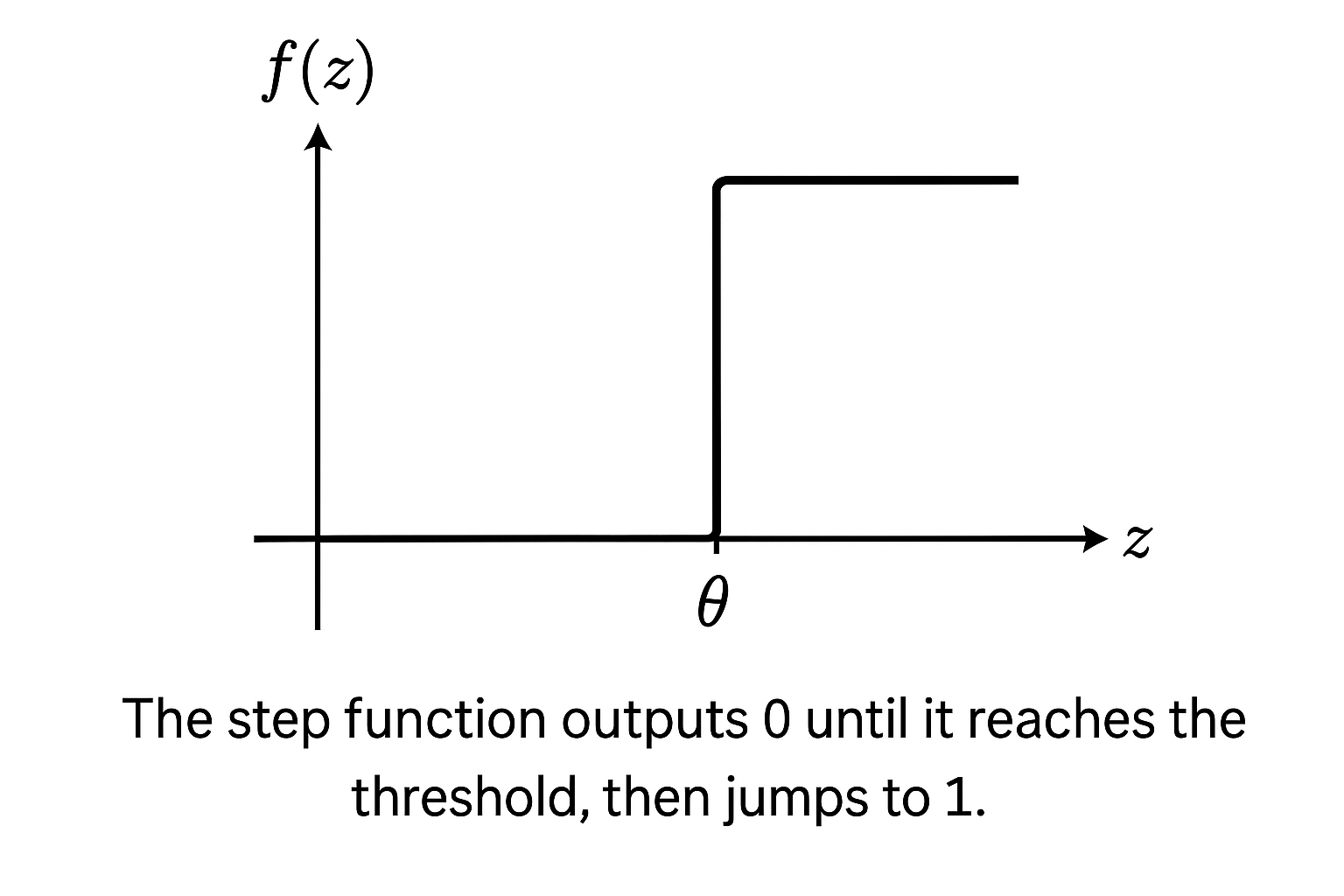
This is how the perceptron draws a line (or plane) to divide data into two classes; by classifying output as one class or another based on if their computed score passes a certain threshold.

---

How Does a Perceptron Learn?

That’s great and all but how does a Perceptron learn to apply the correct weights? The cheesecake/STP example is pretty simple, but real-world problems may have millions or even billions of inputs; crafting weights for them all by hand is cumbersome, and doesn’t really adhere to the concept of machine “learning”.

Rosenblatt’s Perceptron learns via a very simple rule:

$$\begin{aligned} w_i &\leftarrow w_i + \Delta w_i \\ \Delta w_i &= \eta (y - \hat{y}) x_i \end{aligned}$$

Where:

• $\eta$ = learning rate (step size)
• $y$ = true label
• $\hat{y}$ = predicted label
• $x_i$ = input value

If the perceptron is wrong, it nudges the weights toward the correct classification. Over many iterations, this shifts the decision boundary into the right position.

---

From Training to Inference

Once trained, the perceptron freezes its weights. It no longer learns; it applies what it has learned to new inputs. i.e. it “infers” the correct answer to new inputs, hence the term “inference”.

---

Conclusion

In this article, we’ve introduced some basic concepts of AI and ML by examining the Perceptron.

Hopefully, you’ve learned:

• What linear separability means (and why it matters).
• How perceptrons use weights, bias, and a step function to make decisions.
• Why they fail on non‑linear problems like XOR.
• How they learn using a simple precursor to backpropagation

Whilst it may seem quite basic, without hyperbole this is the foundation of all AI/ML technologies that have followed. So it’s good to learn, and future articles in this series will assume this basic knowledge so give it a good read!