Written 05 August 2025 · Last edited 17 September 2025 ~ 16 min read
Activation Functions

Benjamin Clark
Part 2 of 3 in Foundations of AI
Introduction
As covered in the previous article in this series, activation functions take the output of a neuron and turn it into a decision.
But, as covered there, the step activation function falls flat on its face when data is not linearly separable.
So a more detailed overview of the different activation functions available is required before this series moves on to multilayered neural networks. Otherwise, all the little neurons in future diagrams will just be black boxes rather than something you actually understand.
The Goal
By the end of this article, you will understand:
- What activation functions do and why they’re essential to neural networks.
- Why the step function is too limited for modern networks.
- How common activations (sigmoid, tanh, ReLU, Mish) work and their trade‑offs.
- How non‑linearity enables networks to build complex, multi‑layer representations.
What is an activation function?
Activation functions simply transform a neuron’s inputs into an output that is then either passed on through to the next layer of the network, or used to inform the network’s final decision.
The step function, covered in the previous post about perceptrons, is fine and dandy for binary output. But modern neural networks require more nuance than a simple “yes” or “no”. How about a “maybe”, or working with non-linearly separable data?
Having graded activation functions with more nuance is fundamental to producing more advanced neural networks. Rather than simple binary outputs, more advanced activation functions allow neural networks to produce probabilistic scores, discover more nuanced features, and interact with more nuanced data than the Perceptron ever could.
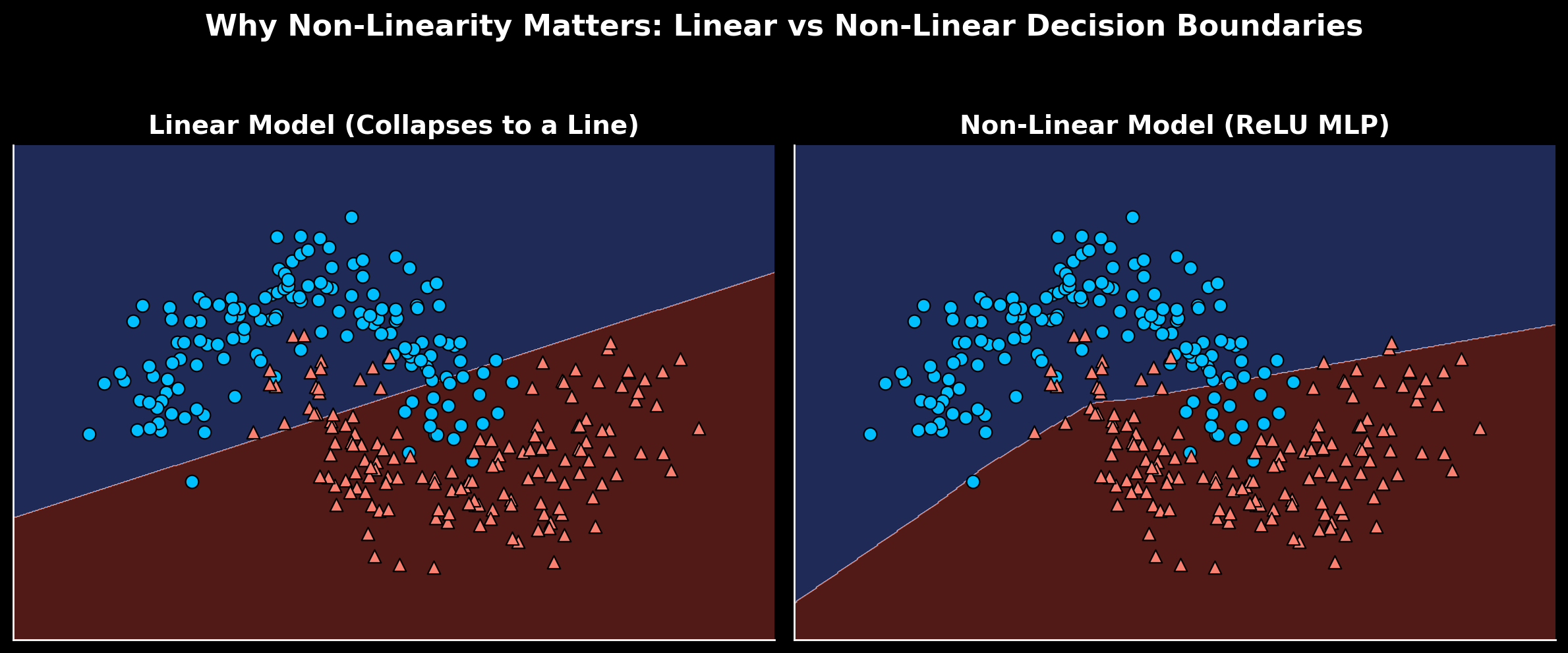
Why Neural Networks Need Non‑Linear Activation
Without non‑linear activations, layering up neurons doesn’t actually expand the network at all; it all collapses into a linear transformation.
Imagine you’re an Eques during the reign of Nero, and a really cushy administrative job has opened in Egypt. You climb the social ladder, do your military service, grease the palm of senators to eventually be considered for the role. However, Nero is famously corrupt and so all this hard work is for naught. When the final decision is made, who gets the job collapses into a singular linear transformation: does Nero like you (1) or not (0)?
For example, if we’re stacking two linear layers:
y=W2(W1x+b1)+b2=(W2W1)x+(W2b1+b2)This simplifies to just one linear transformation — offering no additional representational power compared to a single layer.
Non‑linear activations break this limitation. They allow each layer to reshape the data space in new ways, enabling the network to learn curved, flexible decision boundaries instead of being limited to straight lines or flat planes.
Following on from my Nero example, imagine instead you are an Eques during the Punic Wars. You serve as a Centurion under Scipio Africanus, perform valiantly at the battle of Zama, and are mentioned in dispatches. When you come back from the War you settle down, open a shop, amass some wealth. When election time in the Senate comes round, you fancy your chances and decide to begin climbing the Cursus Honorum. Entering the election for Quaestor, your previous military service, good reputation among the elite, and considerable means all combine to inspire confidence in the electorate and you get the job. The decision didn’t collapse to a linear transformation; many contributing factors compounded to arrive at the outcome.
The Step Function
In the previous article, we introduced the step function — Rosenblatt’s original choice for the perceptron. It outputs either 0 or 1 based on whether the combined input z crosses a threshold:
f(z)={10if z≥θif z<θ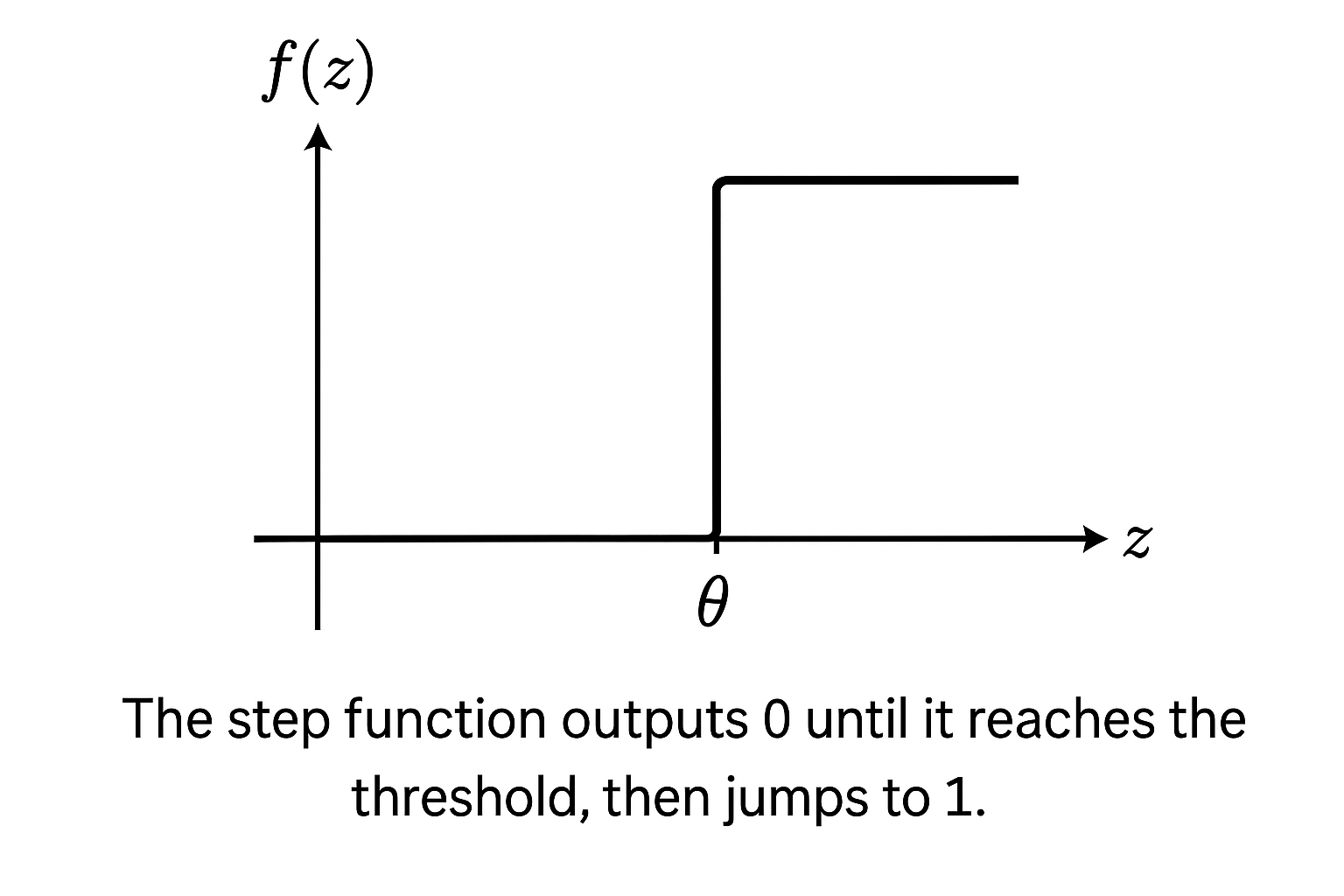
The lack of any gradient to the output, sharp switch between classifications, and restriction to linear boundaries makes it wholly unsuitable for training any network which requires nuance. Researchers quickly replaced it with smoother, differentiable, functions which could support multilayered learning.
Common Activation Functions
Modern activation functions address the limitations of Rosenblatt’s step function. They provide gradients for learning, handle a wider range of inputs, and give networks the expressive power needed for complex tasks.
Each one reshapes inputs differently, offering distinct trade-offs in training speed, stability, and representational power.
Sigmoid
Definition
The sigmoid function maps any real-valued input into a smooth curve between 0 and 1:
f(z)=1+e−z1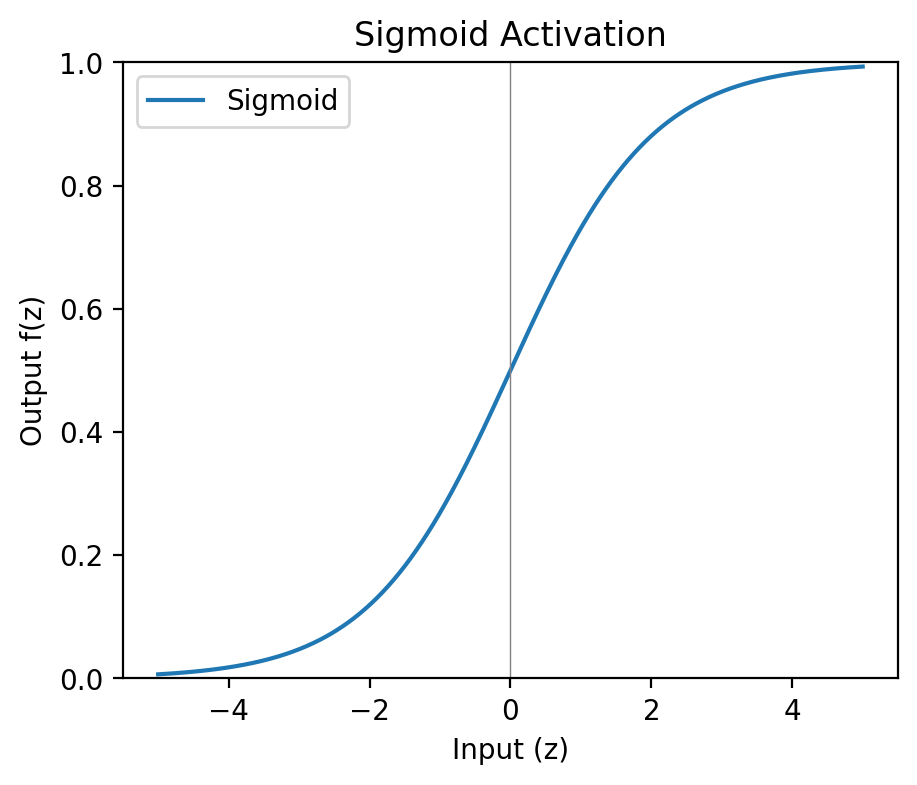
Purpose
This is a softer version of the step function. Small inputs approach 0, large inputs saturate near 1, and there is a smooth transition - rather than a large jump or “step” - between the extremes.
Pros
- Differentiable everywhere. The derivative exists at all inputs, enabling gradient-based learning.
- Outputs values between 0 and 1, making said output interpretable as probability.
Cons
- Suffers from vanishing gradients; extremes flatten the smooth curve between 0 and 1, which has the capability to slow or even halt learning altogether.
- Not zero-centred, meaning that during training optimisation outputs can “zig-zag” between extremes negatively impacting neurons further upstream.
In machine learning, a gradient measures how much a function changes when its inputs change. i.e. in the above image, it may be thought of as the slope of the curve between 0 and 1.
Said gradient informs how to adjust each weight to reduce errors. If we need a higher value, we nudge the weight as appropriate to follow the gradient to a higher score etc.
The overall gradient of learning across all neurons is directly affected by the activation functions used in each layer of the neural network.
In deep networks, some activation functions (like sigmoid and tanh) produce gradients that get very close to zero for extreme input values.
As these small gradients are propagated back through many layers, they shrink further, effectively stopping weight updates.
This is the vanishing gradient problem — one of the key reasons sigmoid fell out of favor for deep networks. i.e. a gradient of 0.000001 isn’t really affected much if you change a weight from 2 to 5.
A zero-centred activation outputs values roughly balanced between negative and positive.
This helps during optimization: when activations are centered around zero, gradients can flow in both directions, leading to faster and more stable convergence.
If an activation function is not zero-centred (like sigmoid) all outputs are positive, meaning bias is created in subsequent layers which further slows down training.
Use cases
- Useful in final output layers for outputting probabilistic distributions.
- Rarely used in hidden layers due to its vulnerability to vanishing gradients and the fact it’s not zero-centred.
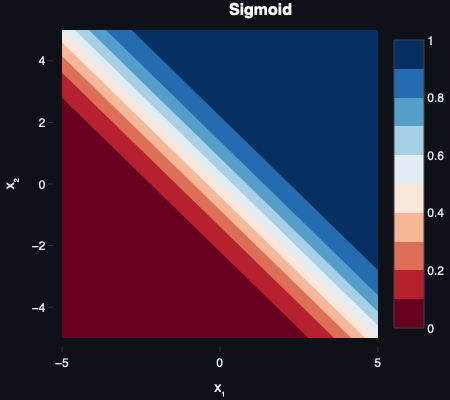
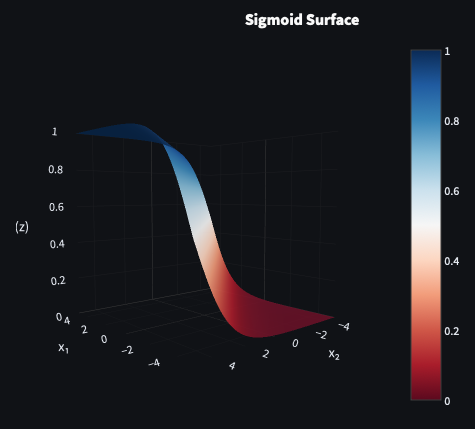
Sigmoid became popular in the 1980s alongside backpropagation, notably in the work of Rumelhart, Hinton, and Williams Learning Representations by Back‑propagating Errors (1986).
Tanh
Definition
The hyperbolic tangent (tanh) function is similar to sigmoid but outputs between -1 and 1, making it zero-centred:
f(z)=tanh(z)=ez+e−zez−e−z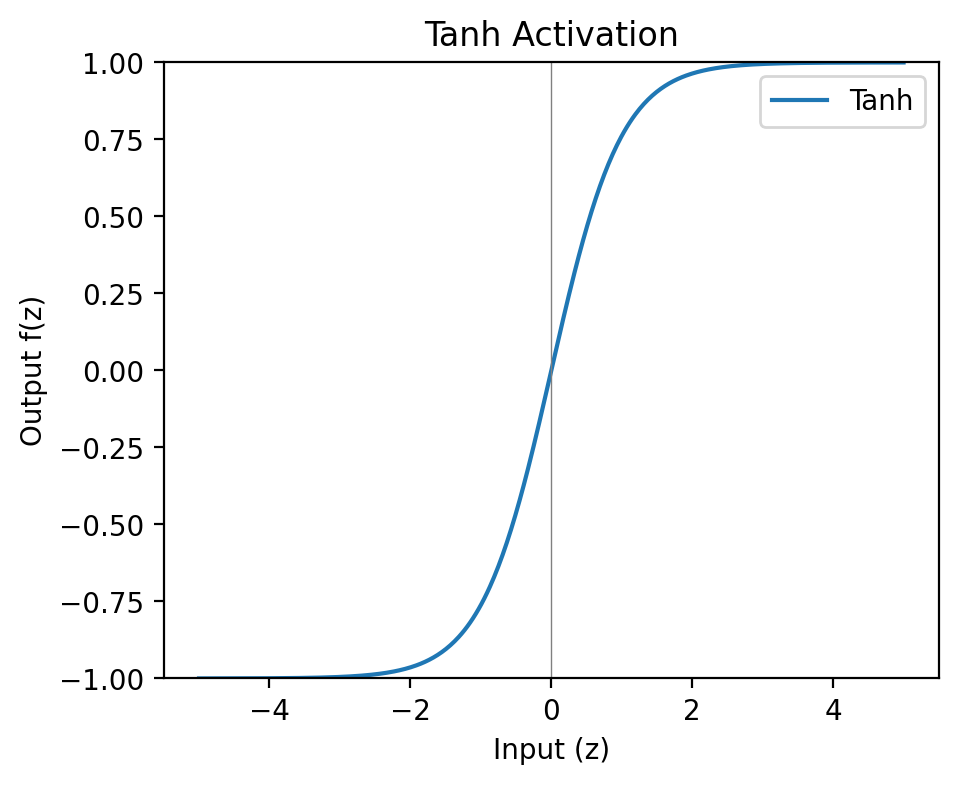
Purpose
Like sigmoid, but centred at zero, allowing for both negative and positive outputs.
Pros
- Zero-centred: Keeps activations balanced, improving gradient flow.
- Smooth and differentiable everywhere.
Cons
- Suffers from the same vanishing-gradient issue as sigmoid at extreme values.
Use cases
- Commonly used in hidden layers for shallow neural networks.
- Still used in recurrent neural networks (RNNs)
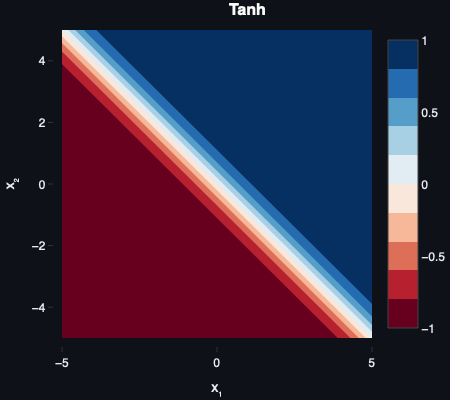
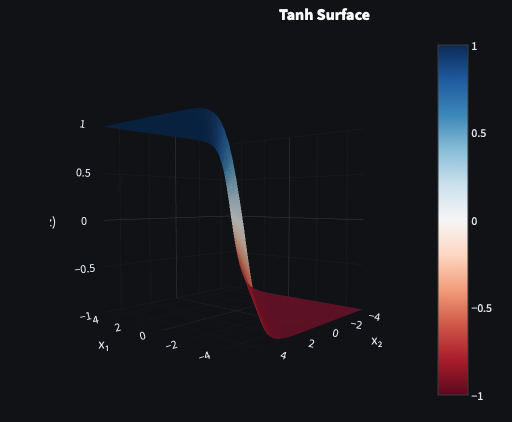
Tanh became a preferred alternative to sigmoid in the late 1980s and was later popularized by Yann LeCun and colleagues in Efficient BackProp (1998).
ReLU
Definition
The Rectified Linear Unit (ReLU) outputs zero for negative inputs and passes positive inputs through unchanged:
f(z)=max(0,z)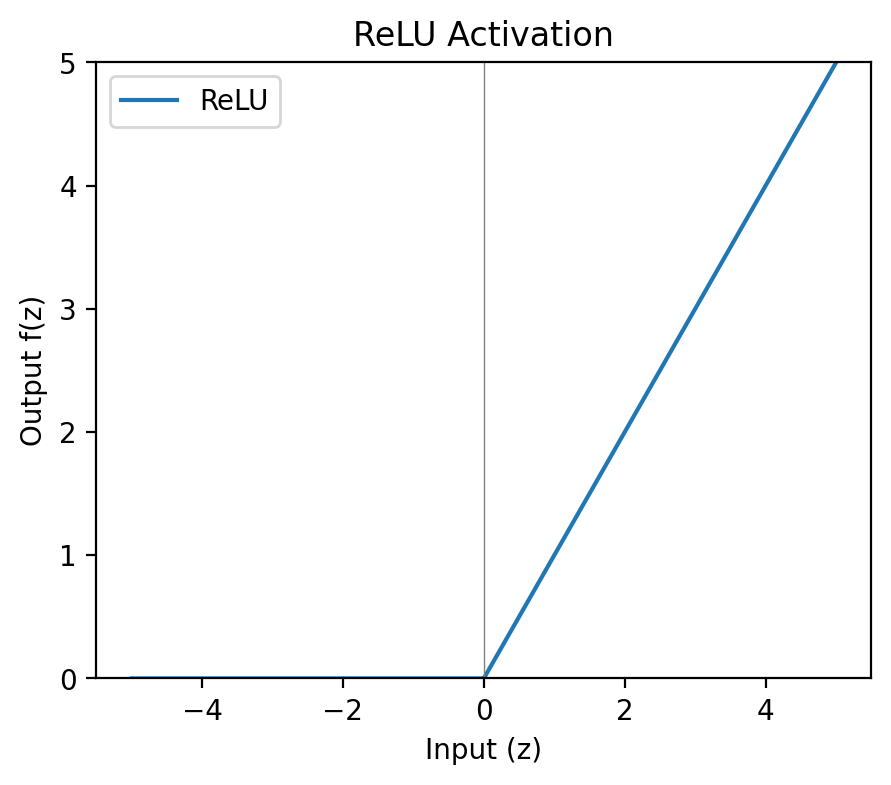
Purpose
Acts as a one-way gate; negative inputs are blocked, whilst positive ones pass through unchanged.
Pros
- Computationally cheap and simple to implement.
- Avoids saturation for positive inputs; they pass through unchanged.
- Works well in deeper neural networks, as the computational effectiveness allows faster training.
Cons
- Dying ReLU problem: neurons can become permanently inactive. Because the output is 0 for negative inputs, if weights are updated
so that a neuron only receives negative inputs, it will always output 0. It effectively “dies” and ceases to contribute to the network.
- Once dead, such neurons may never reactivate, reducing the model’s capacity to learn complex features.
Use cases
- A standard choice for hidden layers in CNNs and MLPs; the original Transformer used ReLU, though many modern variants prefer different activation functions.
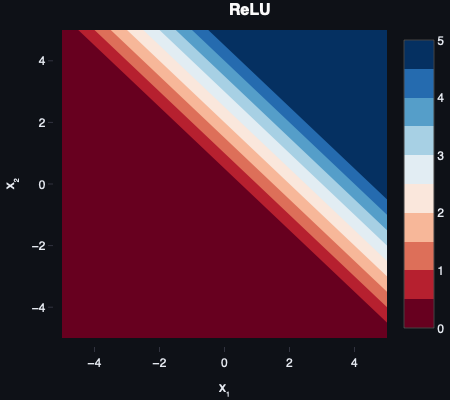
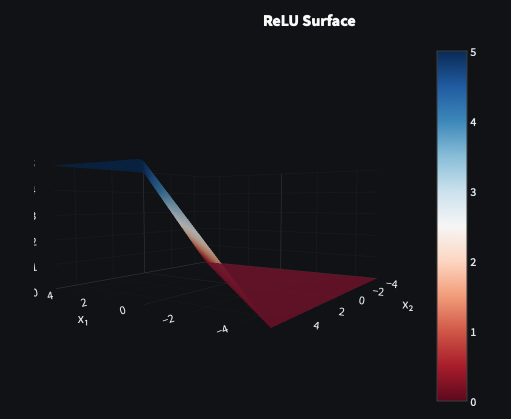
ReLU gained prominence after Nair and Hinton’s Rectified Linear Units Improve Restricted Boltzmann Machines (2010) and was popularized by Krizhevsky et al. in AlexNet (2012).
Leaky ReLU
Definition
Leaky ReLU modifies ReLU by adding a small negative slope for z<0:
f(z)={zαzz≥0z<0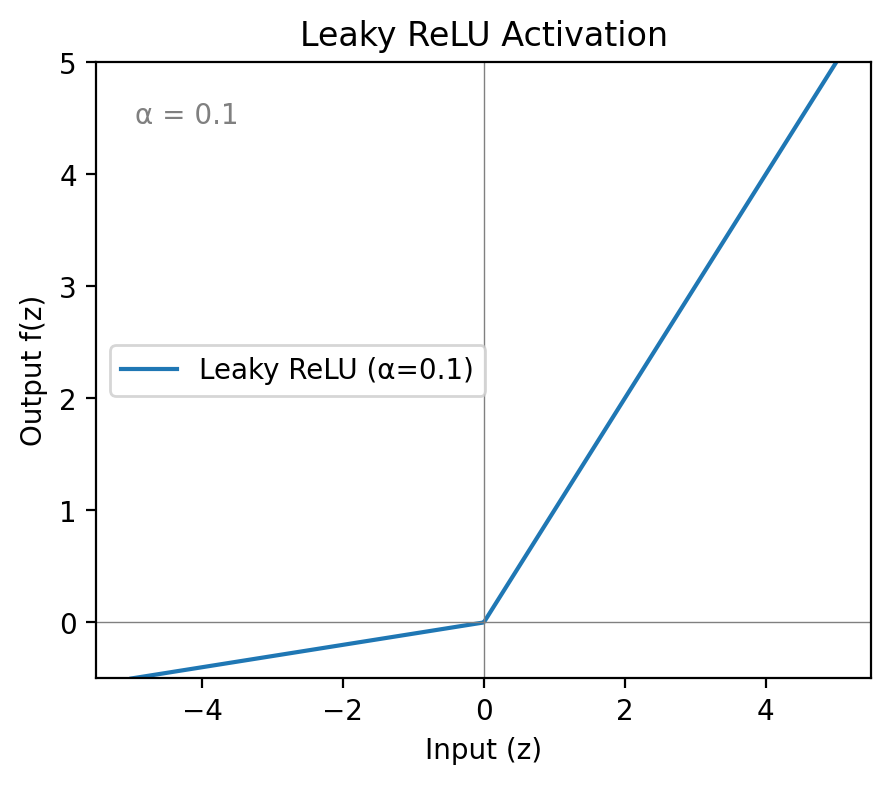
Purpose
By allowing for small negative outputs instead of zero for negative inputs, leaky ReLU helps prevent neurons from dying. Because negative inputs produce non-zero outputs, their weights receive gradients during backpropagation and can still influence the network, rather than passing a zero forward. The “leak” is controlled by α (e.g., α≈0.01 in common setups).
Pros
- Mitigates the “dying ReLU” problem.
- Still fast and efficient.
Cons
- Introduces a hyperparameter α.
A hyperparameter is a value you set before training (like α in Leaky ReLU or ELU) that controls how the model behaves.
These values are not learned from data. Instead, they’re chosen by the practitioner (often tuned via validation) and can significantly influence performance.
Use cases
- Useful when training deep networks that show dying-ReLU or overly sparse activations
Leaky ReLU was introduced by Maas et al. in Rectifier Nonlinearities Improve Neural Network Acoustic Models (2013).
ELU
Definition
The Exponential Linear Unit (ELU) smoothly maps negative inputs toward a small negative value:
f(z)={zα(ez−1)z≥0z<0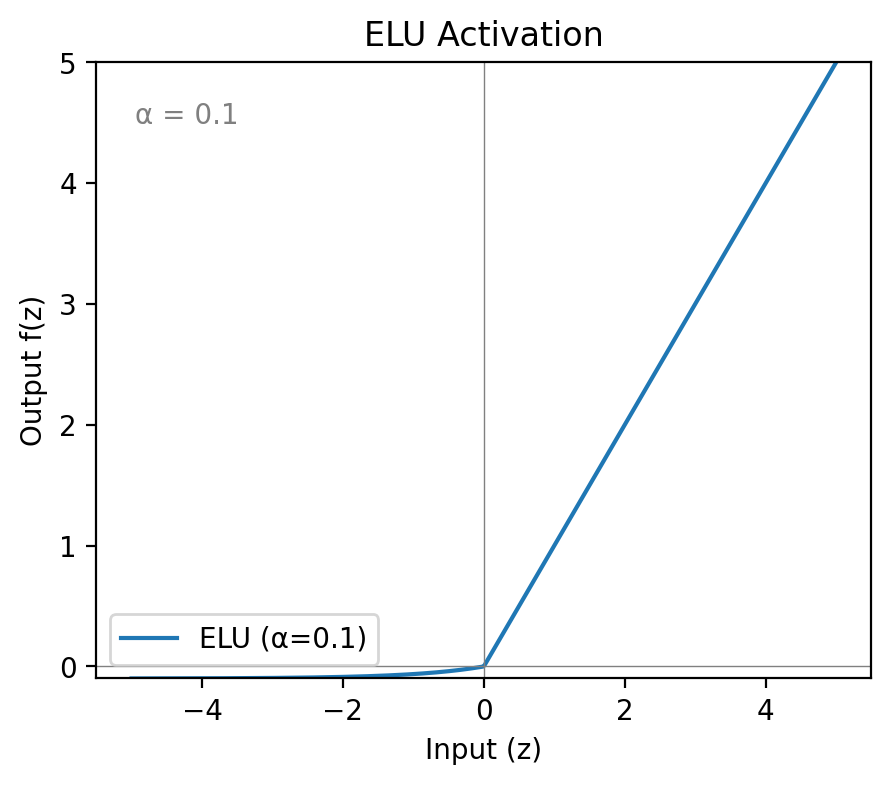
Purpose
By smoothing the negative side, ELU reduces bias shift (mean activation drift) and can stabilise training, at the cost of a slightly higher compute expense than Leaky ReLU (due to the exponential on the negative side).
Pros
- Allows negative outputs, pushing activations closer to zero on average (more zero-centred).
- Smooth, nonzero gradient on the negative side.
Cons
- Slightly more expensive than ReLU (only on the negative side).
- Still requires tuning α.
- Can still exhibit vanishing gradients for very negative inputs as ez→0.
Use cases
- Deep networks where stable convergence is critical. i.e. when you can trade a small compute cost for smoother optimisation.
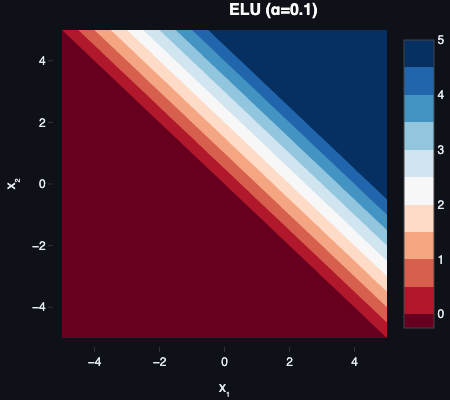
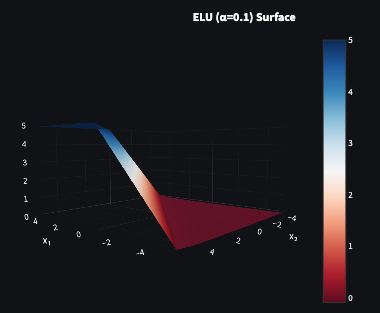
ELU was proposed by Clevert et al. in Fast and Accurate Deep Network Learning by Exponential Linear Units (2015).
Mish
Definition
The Mish activation activation is a smooth, non-monotonic function:
f(z)=z⋅tanh(ln(1+ez))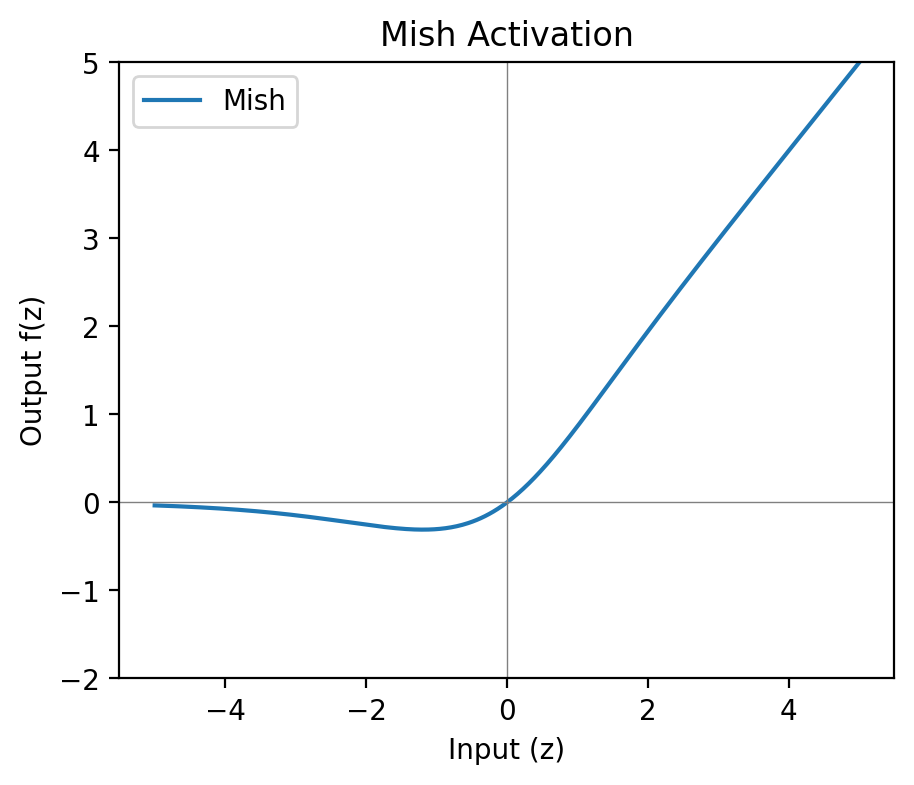
Purpose
Mish behaves like a smooth ReLU variant with better gradient flow and more zero-centred activations. Because it’s non-monotonic, its derivative is negative over a small interval on the negative side. he curve dips slightly before rising, creating a shallow local minimum around z≈−1.19 (value ≈−0.309). This preserves small negative outputs, which has been reported to improve performance in some deep models.
Pros
- Smooth (C∞), non-monotonic, and produces negative outputs (more zero-centred on average).
- Empirically effective in some vision and NLP tasks.
Cons
- More computationally expensive.
- Still relatively new and less widely supported.
Use cases
- Models where you want ReLU-like behaviour on (z>0) with a smooth, informative negative tail.
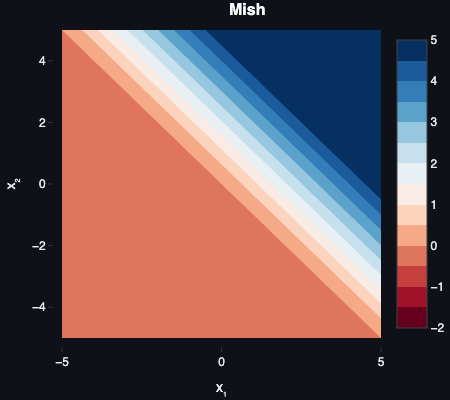
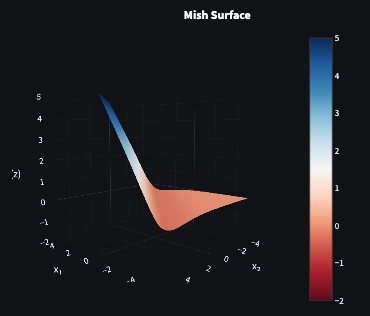
Mish was introduced by Diganta Misra in Mish: A Self Regularized Non-Monotonic Neural Activation Function (2019).
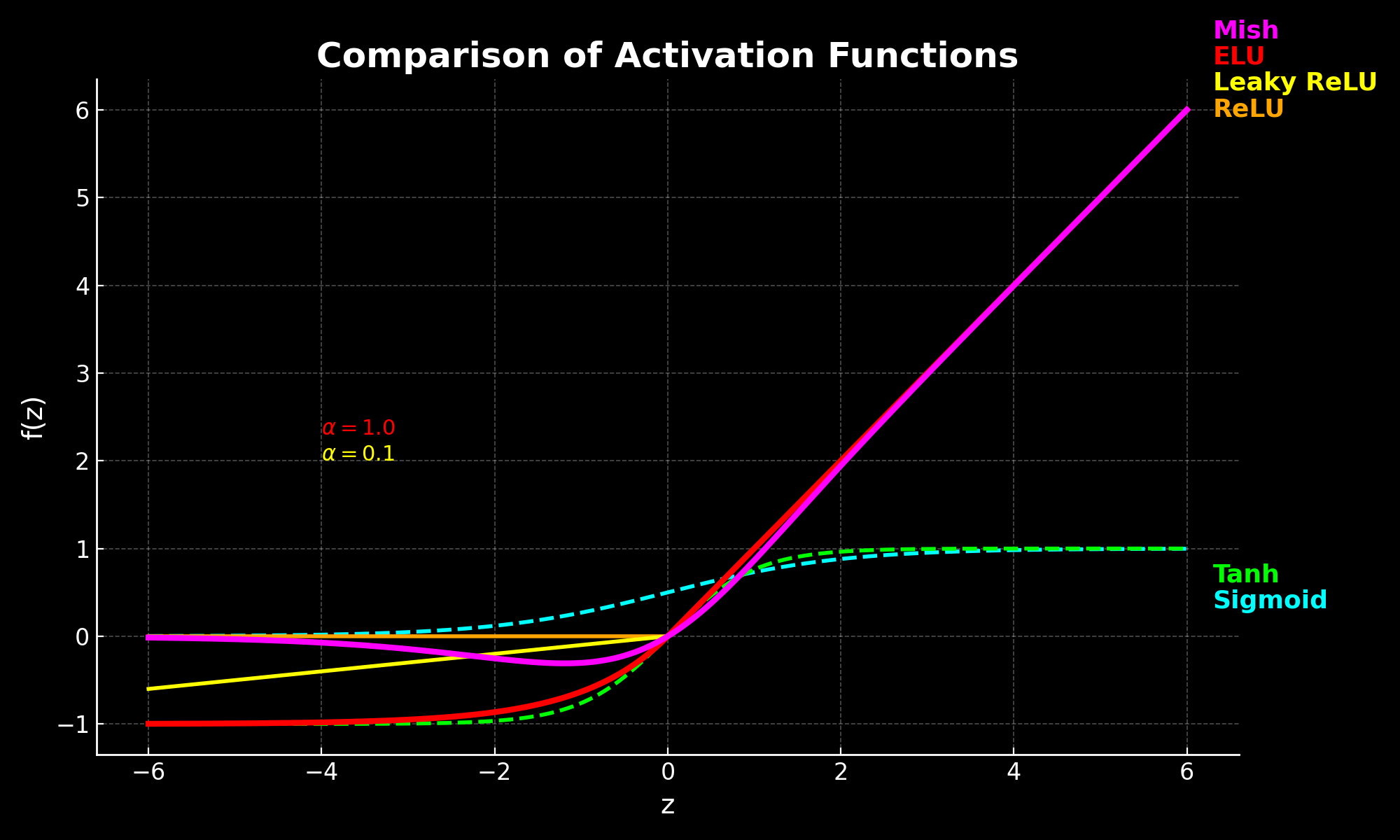
Comparing Activation Functions
Leaky ReLU and ELU include a tunable parameter α. Common defaults: α=0.01 for Leaky ReLU and α=1.0 for ELU.
In Parametric ReLU (PReLU), α becomes learnable, allowing the model to adapt it during training.
Here’s a quick reference comparing the activation functions we’ve covered — their output ranges, whether they’re zero-centred, and why these details matter in practice.
| Function | Output Range | Zero-Centred? | Why It Matters |
|---|---|---|---|
| Step | 0 or 1 | No | Historically important; unsuitable for gradient-based training. |
| Sigmoid | 0 to 1 | No | Smooth; outputs can be interpreted as probabilities (often in output layers). But it saturates, thus suffering from vanishing gradients. |
| Tanh | ‑1 to 1 | Yes | Zero-centred; still saturates at extremes. |
| ReLU | 0 to ∞ | No | Simple and fast; works well in deep nets but can “die” on negative inputs. |
| Leaky ReLU | ~‑∞ to ∞ | Mostly | Allows small negatives which mitigate dying ReLU, which also means its mean activations tend to be closer to zero than ReLU. |
| ELU | ~‑1 to ∞ | Mostly | Smooth negative side, which pushes means towards zero, but slightly slower to compute. |
| Mish | ~‑∞ to ∞ | Mostly | Smooth and non-monotonic, preserving small negatives, but slightly slower to compute. |
How these enable multilayer networks
Earlier in the article, we saw that stacking purely linear layers collapses into a singular affine transformation.
Concretely, consider a single perceptron:
a=f(w⊤x+b)If we want to model complex relationships, a natural idea is to stack perceptrons. But with a linear activation function:
a(1)a(2)=W(1)x+b(1)=W(2)a(1)+b(2)=W(2)(W(1)x+b(1))+b(2)=(W(2)W(1))x+(W(2)b(1)+b(2))This simplifies to a single affine map. However, if we insert a non-linear activation function f between the layers:
a(1)=f(W(1)x+b(1)) a(2)=f(W(2)a(1)+b(2))Now the network no longer collapses to a single affine transformation.
Instead, each layer can reshape the representation non-linearly, allowing the network to model more complex, curved decision boundaries
Imagine building a network to recognise handwritten digits (e.g., MNIST).
- First layer: detects simple features like edges or curves in the pixels.
- Second layer: combines edges into motifs such as loops, lines, and corners.
- Third layer: composes motifs into digit-level patterns (e.g., “3” vs “8”).
Without non-linear activations, each layer would perform another linear transform and these rich, layered features would not emerge. However non-linearity allows layers to build on one another and extract increasingly complex features from the input.
Conclusion
In this article, we’ve examined common activation functions, how they introduce non-linearity, and how this enables neural networks to model complex decision boundaries.
Hopefully, you’ve learned:
- What activation functions do and why they’re essential to neural networks.
- Why the step function is too limited for modern networks.
- How common activations (sigmoid, tanh, ReLU, Mish) work and their trade‑offs.
- How non‑linearity enables networks to build complex, multi‑layer representations.
Have a good read of this, because as I begin to delve into multilayer perceptrons and more exciting things having a good grasp of what activation functions are used, and why, is essential to grokking the rest of it.
Part 2 of 3 in Foundations of AI
